The time-dependent Schrödinger equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system (in terms of its corresponding wave function) changes over time. The Madelung equations are a hydrodynamic interpretation of the Schrödinger equation that result from a nonlinear canonical transformation and a partitioning of the real and imaginary parts.
Check out the Github repository and the presentation slides.
Mathematical Formulation
The time dependent Schrödinger equations read as $$ i\hbar \frac{\partial}{\partial t} \psi = \left( - \frac{\hbar^2}{2m} \nabla^2 + V \right) \psi \tag{1} $$ which can be rearranged as $$ \nabla^2 \psi - \frac{2m}{\hbar^2} V \psi + i \frac{2m}{\hbar} \frac{\partial \psi}{\partial t} = 0 \tag{2} $$ We then take the Madelung transformation $\psi = \sqrt{\rho}e^{\frac{i\theta}{2}}$, which, for now, we write as $\psi = \alpha e^{i \beta}$. This gives us $$ \nabla^2 (\alpha e^{i \beta}) - \frac{2m}{\hbar^2} V (\alpha e^{i \beta}) + i \frac{2m}{\hbar} \frac{\partial}{\partial t}(\alpha e^{i \beta}) = 0 \tag{3} $$ where $\alpha \equiv \alpha(\vec x, t)$ and $\beta \equiv \beta(\vec x, t)$. If we then split this into real and imaginary parts, after applying chain and product rules, we obtain
| Term in $(3)$ | $\nabla^2$ | $V$ | $\frac{\partial}{\partial t}$ |
|---|---|---|---|
| Real | $e^{i\beta} \nabla^2 \alpha - e^{i\beta} \alpha \nabla \beta \cdot \nabla \beta$ | $-\frac{2m}{\hbar^2} V \alpha e^{i\beta}$ | $-\alpha \frac{2m}{\hbar} \frac{\partial \beta}{\partial t} e^{i\beta}$ |
| Imaginary | $ie^{i\beta} \alpha \nabla^2 \beta + 2ie^{i\beta}\nabla \alpha \cdot \nabla \beta$ | $0$ | $i \frac{2m}{\hbar} \frac{\partial \alpha}{\partial t} e^{i \beta}$ |
We can factor out $e^{i \beta}$ from the real part, and $ie^{i \beta}$ from the imaginary part, yielding $$ \nabla^2 \alpha - \alpha \nabla \beta \cdot \nabla \beta - \frac{2m}{\hbar^2} V \alpha - \alpha \frac{2m}{\hbar}\frac{\partial \beta}{\partial t} = 0 \tag{4.1} $$ $$ \alpha \nabla^2 \beta + 2 \nabla \alpha \cdot \nabla \beta + \frac{2m}{\hbar} \frac{\partial \alpha}{\partial t} = 0 \tag{4.2} $$
Consider equation $(4.2)$. If we take $\varphi = -\frac{\beta \hbar}{m}$, and noting that $\frac{\partial (\alpha^2)}{\partial t} = 2 \alpha \frac{\partial \alpha}{\partial t}$, we find $$ \frac{\hbar}{m}\alpha^2 \nabla^2 \beta + 2 \frac{\hbar}{m} \alpha \nabla \alpha \cdot \nabla \beta + \frac{\partial}{\partial t} \alpha^2 = \alpha^2 \nabla^2 \varphi + 2 \alpha \nabla \alpha \cdot \nabla \varphi + \frac{\partial}{\partial t} \alpha^2 \tag{5.1} $$ $$ = \nabla \cdot (\alpha^2 \nabla \varphi) + \frac{\partial}{\partial t} \alpha^2 = 0 \tag{5.2} $$ which, notably, can be interpreted as a conservation equation where $\alpha^2$ is the density of the fluid and $\nabla \varphi$ is the fluid velocity field.
Similarly, equation $(4.1)$ gives us $$ \frac{\partial \varphi}{\partial t} - \frac{\hbar^2}{2m^2}\frac{\nabla^2\alpha}{\alpha} + \frac{1}{2}\nabla \varphi \cdot \nabla \varphi + \frac{V}{m} = 0 \tag{6} $$ which corresponds to the integral of the Euler equations for irrotational flow. Because $\nabla \times \vec u = \nabla \times \nabla \varphi = 0$, taking the gradient yields the familiar Euler equation, $$ \frac{\partial u}{\partial t} + \vec u \cdot \nabla u = -\frac{1}{m} \nabla \left(V - \frac{\hbar^2}{2m} \frac{\nabla^2 \alpha}{\alpha} \right) \tag{7} $$
In line with the corresponding hydrodynamic interpretation of equation 5.2 and 7, we write the full Madelung equations as $$ \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec{v}) = 0, \quad \frac{\partial \vec{v}}{\partial t} + (\vec{v} \cdot \nabla)\vec{v} = -\frac{1}{m}\nabla (Q + V) \tag{8} $$ where $\rho$ is the mass density, $\vec{v}$ is the velocity field, $Q$ is the Bohm quantum potential, $V$ is the potential energy, and $\psi$ is the wave function. $$\rho = m|\psi|^2 \tag{9}$$ $$Q = -\frac{\hbar^2}{2m}\frac{\nabla^2 \sqrt{\rho}}{\sqrt{\rho}} \tag{10}$$
Evaluation using Smoothed-Particle Hydrodynamics
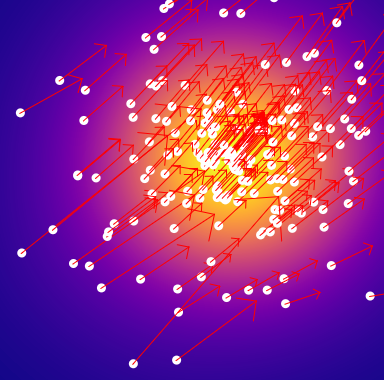
We discretize the Madelung Equations using a technique common to classiscal computational fluid dynamics: smoothed particle hydrodynamics (SPH). One benefit of SPH over mesh-based methods is that it is a Lagrangian method, which is useful for adapting to complex or unbounded domains. Our implementation follows that outlined by Mocz and Succi, 2015, adapted to two dimensions.
SPH leverages a kernel convolution to discretize a field $$ A(\vec x) = \int A(\vec x’) \delta(\vec x - \vec x’) dx’ \tag{11} $$ where $\delta$ is the Dirac delta function. We approximate the Dirac delta with a Gaussian smoothing kernel, whose integral over space is 1 $$ W(\vec x; h) = \frac{1}{\pi h^2} \exp \left(- \frac{| \vec x |^2}{h^2} \right) \tag{12} $$ with smoothing length $h$ such that $\lim_{h \rightarrow 0} W = \delta$. To that end, alternative kernels that have compact support (i.e. go to 0 at a distance of $h$) are less computationally expensive, but also less accurate.
We approximate fields by its smoothed average over N particles $$ A(\vec x) \approx \langle A(\vec x) \rangle = \sum_j \frac{m_j}{\rho_j} A(\vec x_j) W(\vec x - \vec x_j; h) \tag{13} $$ where the $j$ index references the $j$th particle. We can approximate gradients and higher order derivatives by shifting the operator to the kernel, whose derivatives are analytically known.
Plugging this into the Madelung equations, we obtain the following discretized equations to be solved for each particle $i$:
-
Acceleration update: $$ \frac{d \vec u_i}{d t} = -\frac{\nabla V}{m} - m \sum_j \left( \frac{P_i}{\rho_i^2} + \frac{P_j}{\rho_j^2} \right) \nabla W_{ij} \tag{14} $$
-
Velocity update: $$ \vec u_i^{n+1} = \vec u_i^{n} + \frac{d \vec u_i}{d t} \Delta t \tag{15} $$
-
Position update: $$ \vec x_i^{n+1} = \vec x_i^{n} + \vec u_i^{n+1} \Delta t \tag{16} $$
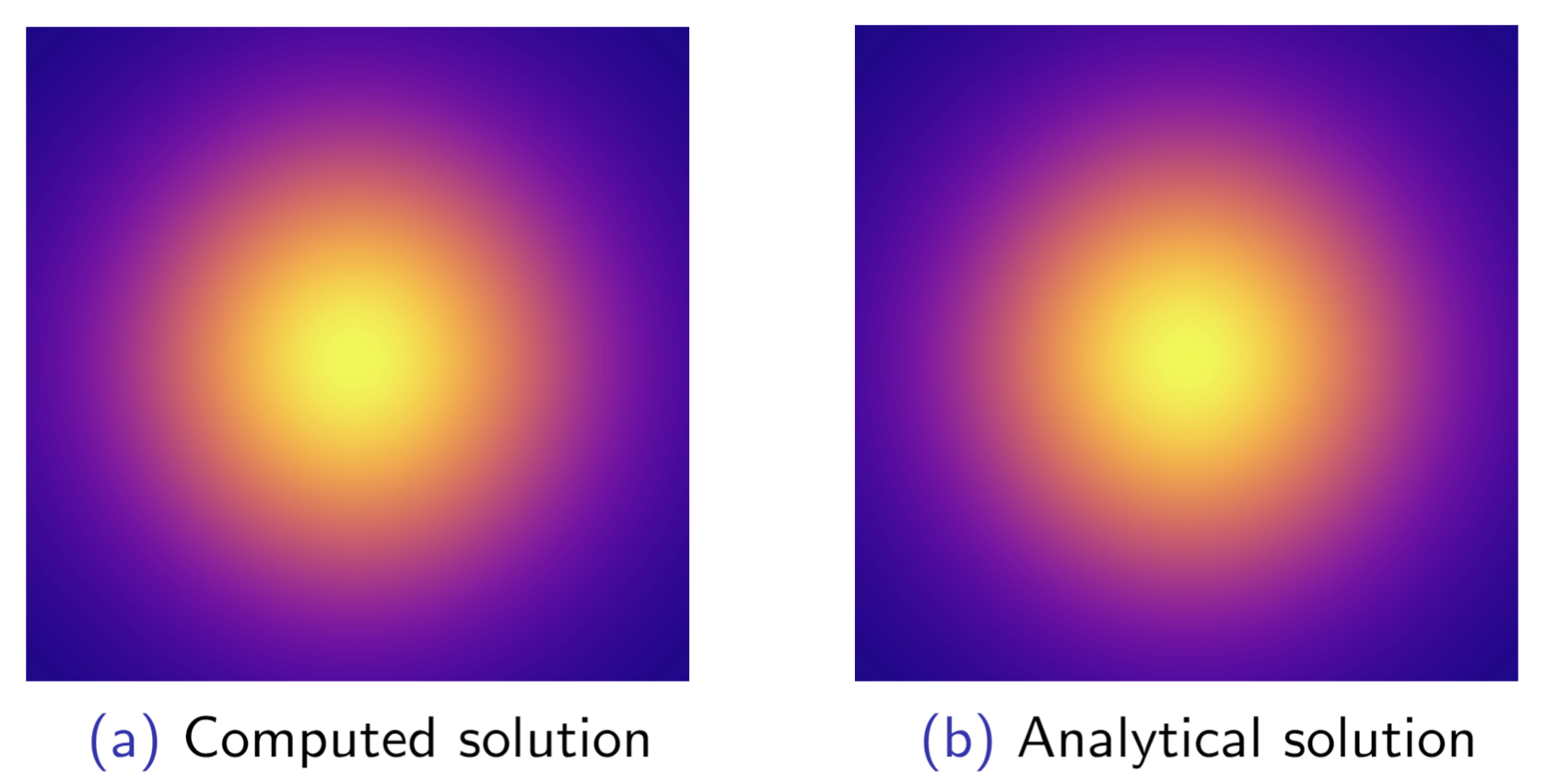
Results