Check out the poster here.

Abstract

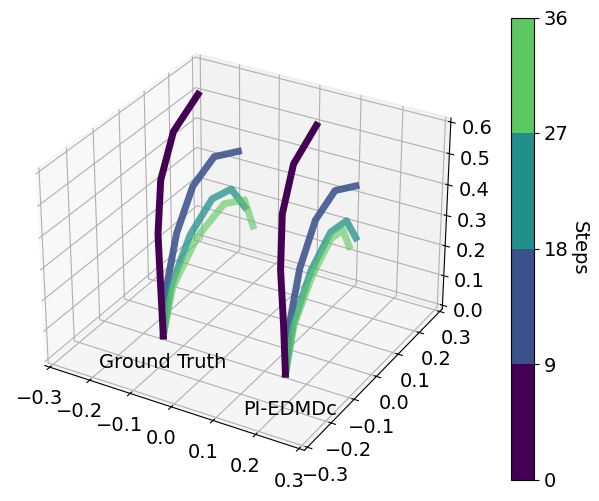
Existing methods for soft robotic control rely on either large quantities of data or computationally expensive numerical simulations, which makes real-time control intractable and potentially dangerous to human operators. In this research, a new method is proposed which combines the efficiency of data-driven methods with the physical accuracy of numerical simulations, thereby reducing necessary data requirements while improving prediction accuracy. This enables soft robots to function effectively in real-time scenarios, improving their overall utility and their safety when working near human operators. Future work involves integrations of this method into more complicated soft robotic systems where their governing physical equations are not necessarily fully known.

Brief Background on Koopman Operators

Consider a dynamical system whose time evolution is described by $$ \dot{\mathbf{x}} = \mathbf{f}(\mathbf{x}, \mathbf{u}) $$ where $\mathbf{x} \in \mathcal{X}$ describes the state of the system evolving on some smooth manifold $\mathcal{X}$, $\dot{\mathbf{x}}$ denotes the time derivative of $\mathbf{x}$, $\mathbf{u} \in \mathcal{U}$ describes the inputs to the system on a smooth manifold $\mathcal{U}$, and $\mathbf{f}: \mathcal{X} \times \mathcal{U} \rightarrow \mathcal{X}$ is a vector field that characterizes the dynamics. In the context of robotics, $\mathbf{x}$ can be thought of the state of some robot, and $\mathbf{u}$ as the applied actuation. Further, one can consider $\mathbf{x} \in \mathbb{R}^n$ and $\mathbf{u} \in \mathbb{R}^m$, where $\mathbf{u}$ is not assumed to be constrained to a smooth manifold. In discrete time, the system is propagated forward in time by the flow map $$ \mathbf{x}(t_0 + t) = \mathbf{F}_t(\mathbf{x}(t_0), \mathbf{u}(t_0)) = \mathbf{x}(t_0) + \int_{t_0}^{t_0 + t} \mathbf{f}(\mathbf{x}(\tau), \mathbf{u}(\tau)) d\tau $$

The Koopman operator $\mathcal{K}_t$ is an infinite-dimensional linear operator that acts on functions $g: \mathcal{X} \times \mathcal{U} \rightarrow \mathbb{R}$ called observables which are elements of some infinite-dimensional Hilbert space $\mathcal{H}$, typically the Lebesgue square-integrable functions. In particular, the Koopman operator propagates measurements of state forward in time, as $$ \mathcal{K}_t g = g \circ \mathbf{F}_t $$ where $\circ$ is the function composition operator. Importantly, the infinitesimal generator of the Koopman operator is also a linear operator, given by the Lie derivative $$ \dot{g} = \lim_{t \rightarrow 0} \frac{\mathcal{K}_t g - g}{t} = \mathcal{L} g = \nabla_\mathbf{x} g \cdot \mathbf{f} + \nabla_\mathbf{u} g \cdot \dot{\mathbf{u}} $$ where the last equality arises from the fact that $\mathcal{L}$ is a Liouville operator. As a simplification, we can assume that over a single time step $\mathbf{u}$ is constant, and thus its time derivative is $0$. Here, $\mathcal{L}$ is sometimes referred to as the continuous-time Koopman operator, whereas $\mathcal{K}_t$ is referred to as the discrete-time Koopman operator.