Check out the thesis in the ASU digital library.

Copy of the thesis is available here.

The slides from the thesis defense are available here.

Check out the code on Google Colab.

Abstract

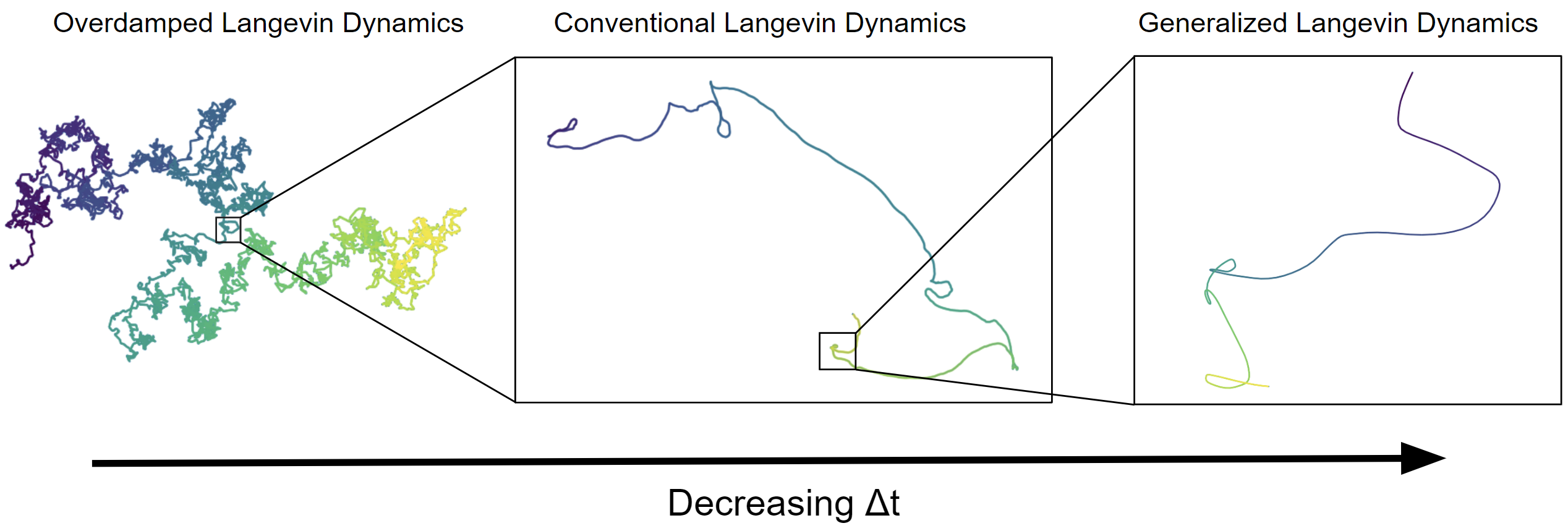
The timescale of a simulation, determined by its size of time step, is an incredibly important consideration for resolving quickly varying dynamics. Indeed, if one chooses an observation timescale larger than the fastest forces in a dynamical system, the intricate details produced by that force’s fluctuations are lost. As such, for large time steps, we require integrators that are capable of capturing the effect of these missed forces, perhaps in a statistical sense if not exactly. This problem is difficult to solve in general. As such, for simulations where these high frequency details do not need to be resolved, lower order models must be employed that resolve the overall effect of these high frequency details by construction. A representative example of this is the modeling of molecular dynamics and Brownian motion. High order models of Brownian motion, such as the generalized Langevin equations, are computationally infeasible when one wants to resolve the dynamics of, for example, a pollen particle in water. A more reasonable choice of model might be the Langevin equations or even further, the overdamped Langevin equations. As a case study, by posing the generalized Langevin equations as a relaxation system, we show how in choosing the size of time step, we automatically reduce to the effective model, without ever explicitly choosing the model used.